Time Series Analysis (Lecture 2): Choosing Optimal Lags in Stata

General Overview on Lag Selection

Since this blog is tailored for beginners in econometrics, I will not be engaging an advanced discussion on the topic but an introductory approach by which a beginner can understand the essence of using lags in a model and the pitfalls that may occur if lags are excessively used. Interested readers who require advanced information on selecting optimal lags can consult appropriate econometric textbooks. Having said that, in economics the dependence of a variable Y (outcome variable or regressand) on another variable(s) X (the predictor variable or regressor) is rarely instantaneous. Very often, Y responds to X with a lapse of time. Such a lapse of time is called a lag. Therefore, in time series analysis, some level of care must be exercised when including lags in a model.

So how many lags should be used in a model? There is no hard-and-fast-rule on the choice of lag length. It is basically an empirical issue. As noted in Damodar Gujarati Basic Econometrics, there is no a priori guide as to what the maximum length of the lag should be. The researcher must bear in mind that, as one estimates successive lags, there are fewer degrees of freedom left, making statistical inference somewhat unstable. Economists are usually not that lucky to have a long series of data so that they can go on estimating numerous lags. More importantly, in economic time series data, successive values (lags) tend to be highly correlated increasing the likelihood of multicollinearity in the model.

Also, from Jeffery Wooldridge’s Introductory Econometrics: A Modern Approach with annual data, the number of lags is typically small, 1 or 2 lags in order not to lose degrees of freedom. With quarterly data, 1 to 8 lags is appropriate, and for monthly data, 6, 12 or 24 lags can be used given sufficient data points. Again, in the words of Damodar Gujarati Basic Econometrics “the sequential search for the lag length opens the researcher to the charge of data mining”. He further stated that the nominal and true level of significance to test statistical hypotheses becomes an important issue in such sequential searches”. For instance, if the lag length, k, is incorrectly specified, the researcher will have to contend with the problem of misspecification errors. In addition, because of the lags involved, distributed and or autoregressive models raise the topic of causality in economic variables.

Hence, before you estimate a time series equation, it is necessary to decide on the maximum lag length. Like I mentioned earlier, this is purely an empirical question. Suppose there are 40 observations in all, by including too many lagged values, your model consumes degrees of freedom, not to mention introducing the likelihood of multicollinearity occurring. As noted in my previous tutorial on multicollinearity, it leads to imprecise estimation; that is, the standard errors tend to be inflated in relation to the estimated coefficients. As a result, based on the routinely computed t ratios, we may tend to declare (erroneously), that a lagged coefficient(s) is statistically insignificant. In the same vein, including too few lags will lead to specification errors. The easiest way out of this quagmire, is to decide using a criterion like the Akaike or Schwarz and choose that model that gives the lowest values of these criteria. Most econometric packages easily compute these optimal lag length but note some trial and error is inevitable.

Choosing Optimal Lags in Stata

For this tutorial, I will extract data from Gujarati and Porter Table 21.1 dataset. It is a quarterly data on United States from 1970 to 1991, which is 88 observations. The variables are gdp (gross domestic product), pdi (personal disposable income) and pce (personal consumption expenditure).

Step 1: Load data into Stata

 

Stata Dataset
Source: CrunchEconometrix

 Step 2: Prepare Stata for Analysis

Inform Stata that you are about to perform a time series analysis by typing this code into the Command box: tsset qtrly

and you will obtain this response:

Stata - tsset Command
Source: CrunchEconometrix

Stata now recognises that you are about conducting a time series analysis using quarterly data from 1^st quarter of 1970 to the 4^th quarter of 1991. If you don’t issue this command, Stata will not run your analysis.

Step 3: Obtain Model Lag Length

Type this code into the Command box: varsoc gdp pce pdi

…and the Stata output for the model (shown below) indicates that lag 2 is the optimal lag and that AIC is the best criterion for the model given it has the lowest value, 26.8144.

Stata - Optimal Lags for the Model
Source: CrunchEconometrix

Step 4: Obtain Variables Lag Length

Optimal lags can be obtained for the respective variables and the rule-of-thumb remains the same. We select that lag identified by the criterion which gives the lowest value.

So, for gdp, type this code into the Command box: varsoc gdp

…and the Stata output indicates that the optimal lag length for gdp is 2.

Stata - Optimal Lags for gdp
Source: CrunchEconometrix

 To obtain optimal lag for pce, type: varsoc pce

…Stata output indicates that the optimal lag length for pce is 4.

Stata - Optimal Lags for pce
Source: CrunchEconometrix

 varsoc pdi

…Stata output indicates that the optimal lag length for pdi is 1.

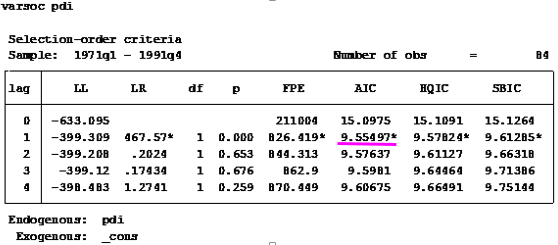Stata - Optimal Lags for pdi
Source: CrunchEconometrix

Caveat: There are also cases where the used lag length is that which is most selected by the criterion named after the econometricians who developed them, like HQ, SIC, AIC and LR, etc. Some researchers prefer Schwartz criterion when the variables are more than 4 and use the AIC when the variables are less than 4. As, mentioned in the introductory part of this tutorial, the decision on the choice of lag is purely an empirical issue. Generally, we choose the lag length for which the values of most of these lag length criteria are minimized, indicated by asterisks in the EViews output.

[Watch video tutorial on lag selection using Stata]

Having gone through this tutorial, it will be easy for you to determine the optimal lag for your model regardless of the analytical package used. The basics are the same. Remember that “Lag length criteria” indicate a definite way of selecting the optimal lag after estimating the initial VAR model (in EViews). Also VAR and ARDL models are susceptible to arbitrary use of lags as this may erode the degrees of freedom, weaken the significance of the coefficients, may induce auto-correlation and weaken the strength of diagnostic tests.

Try these steps on your models and if there are further and comments, do post them below…..