Two-way ANOVA Procedure using Stata
This is a
follow-up to my previous post on how to analyse the one-way ANOVA using Stata analytical software endeavour to read it up...it also provides a good
introduction to running ANOVA.
The
essence of two-way ANOVA in data analysis
ANOVA simply means analysis of
variance
and its importance in analysing behavioural relationships between and among
variables makes its use endearing to researchers. Basically, the ANOVA procedure
is to determine if the average value (that is, the mean) of a dependent variable (the regressand,
outcome variable, and endogenous variable) is the same in two or more
unrelated, independent groups. That
is, the two-way ANOVA indicates whether the mean of a dependent variable is the
same or differs across independent unrelated categorical groups. The
two-way ANOVA compares the mean differences between groups that have been split
on two independent variables (called factors).
The primary purpose of a two-way ANOVA is to understand if there is an interaction between the two independent
variables on the dependent variable. The moment you understand how to compute the two-way ANOVA and interpret
your table, you will always want to incorporate it in your study or research…after
ensuring that your data meets some salient conditions.
For
instance, you could use a two-way ANOVA to understand whether there is an interaction between activity level and
diet on bmi (i.e. the dependent variable would be “bmi”, measured on a continuous scale, and your independent
variables would be “activity level” (which has three groups – “low”,
“moderate” and “high”) and “diet” (which
has three groups “vegan”, “vegetarian” and “animal-based”). Again, the two-way
ANOVA can be used understand if there is an interaction between demographic
location and types of housing on rentals (i.e. the dependent variable would be
“rentals”, measured on a continuous
scale, and the independent variables would be “location” (which has two groups – “rural” and “urban”) and “housing types” (which has six groups “one-room
apartment”, “two-room apartment”, “one-bedroom condo”, “two-bedroom condo”,
“mini flat”, and “standard flat”). Lastly, an agronomist may be interested in
knowing the interaction between temperate conditions and type of fertiliser on
say the crop yield of cassava (i.e. the dependent variable would be “yield”, measured on a continuous scale,
and the independent variables would be “temperate”
(which has four groups – “autumn”, “spring”, “summer” and “winter”) and “fertiliser” (which has two groups
“organic”, and “inorganic”). If there are three independent variables rather
than two, a three-way ANOVA will be performed, and if four independent
variables, a four-way ANOVA will be performed and so on
Given this preamble, here is a “step-by-step”
tutorial showing you how to carry out a two-way ANOVA and some post-hoc checks
using Stata analytical package. But before I proceed, it is important for you
to understand some basic rules underlying the use of two-way ANOVA procedure.
That is, your data must meet these criteria failing which your results may be
invalidated if they are not adhered to. There are six (6) of them:
Rules:
These six "rules" represent the blueprint
guiding the use of the two-way ANOVA technique. If any is not satisfied, you
may obtain invalid results. Please note that the first three assumptions are
closely related to the nature of your data and study structure (that is,
directly related to your choice of variables), thus Stata cannot validate those
while the last three must be met using some Stata criterion. It is therefore
important that you ascertain that your study meets these conditions before
proceeding with the two-way ANOVA.
·
Rule #1: Make sure that the dependent variable (regressand,
outcome variable) is cardinal and measured in continuous terms. Some
example of variables measured in continuous terms are: time (measured in minutes,
seconds, and milliseconds), weight (measured in stone, pounds, kilogramme, and
grams); rentals (measure in local currency) and so on. These are called continuous variables.
·
Rule #2: Both explanatory variables (regressor,
independent variable) ought to comprise two or more categorical, independent
(unrelated) groups. Some examples of these categorical variables
are income group (3 groups: high-income, middle income and low income); grade
(4 groups: excellent, very good, good, and poor); demography (2 groups: rural
and urban); banking (3 groups: investment, mortgage, microfinance) etc. So make
sure that your explanatory variable is a categorical variable.
· Rule #3: Ensure that you have independence of observations. That is, your
observations must not over-lap across the different groups. This simply means
that there must be no relationship between the observations in each group or
between the groups themselves. For instance, an observation in a “winter” group
must not be represented again
in a “spring” group. Needless to say that, participants across the groups must
be different. But where an exception is the case, the repeated measures of
ANOVA should be used rather than the two-way ANOVA.
· Rule #4: Be wary of conspicuous outliers. These are figures that are
either abnormally high or low, that is, they do not follow the typical pattern
in a particular variable. The presence of outliers can bias your results, they
can have a negative effect on the two-way ANOVA, thereby reducing the results
accuracy. However, they can easily be tested in Stata by
using the Boxplot or summary syntax (sum for short). The syntax computes the mean, standard deviation,
minimum and maximum values in each variable in your data, thus enabling you to
detect (identify) the abnormal figure.
·
Rule #5: Since the two-way ANOVA is susceptible to
violations of normality, it is essential that the dependent variable
must be approximately normally distributed for each category of the
independent variable. Although, you may still obtain some valid results if
this rule is violated, that is why your data must be approximately and
not 100%
normally distributed before running a two-way ANOVA. A histogram test, Shapiro-Wilk test or Jarque-Bera test can be conducted in
Stata to test for normality of residuals.
· Rule #6: There must be homogeneity of variances. This can be tested with
the Levine’s test for homogeneity of
variances in Stata. The Levine’s test is very vital when it comes to
interpreting the results from a two-way ANOVA guide because Stata is capable of
producing different outputs depending on whether your data meets or fails this
assumption.
Note: The first three rules are
specific to your data, choice of variables and nature of study which any
analytical package, like Stata, has no control and thus cannot be
scientifically verified. However, ascertaining that your data meets the last
three rules can be verified which may seem daunting, but it is important that
you do them. Moreso, these packages have really simplified these procedures.
So let us take an example to understand the two-way
ANOVA….
EXAMPLE
From
Wooldridge’s discrim2.dta or discrim2.xlsx files (if you don’t have Stata
installed on your devise, download the .xlsx file and feed into the analytical
package of your choice).
(Note: for simplicity, I have
extracted from the initial dataset, discrim.dta, to use for this example. The
initial dataset is quite detailed such that several two-way ANOVA simulations
can be carried out).
A researcher collected ZIP code-level data on the prices charged
for small fries at four fast-food chains – Burger King, Kentucky Fried Chicken,
Roy Rogers and Wendy’s – along with the characteristics of the ZIP-code
population in two US states – New Jersey and Pennsylvania. The idea is to
compare the prices charged by these fast-food chains to see whether the prices
are the same across the two states.
In this example, the dependent variable is “price of fries” (measured in US
dollars), whilst the independent variables are “state” and “chain”. state has two independent groups: “New Jersey” and “Penn” and “chain” has
four independent groups: “BK”, “KFC”, “RR” and “WD”. Remember
that both are categorical variables whose members (observations) must not
over-lap within their groups. The two-way ANOVA in this instance, is used to
determine whether there is a statistically significant difference in prices
charged among the four fast-food chains across the two states.
But before we begin, ensure that you set up your
data in Stata (or any analytical package of your choice)
Setting up the data in Stata
1.
Ensure original data is in excel format (.xlsx,
.xls or .csv)
2.
Have separate columns for prices of fries, state
and chain
3.
Open the Stata
application
4.
Go to Data
>> Data Editor (Edit)
5.
Highlight data to be copied from excel
6.
Click the “paste”
icon in Stata
7.
A dialog box opens: Select “Treat first row as variable names”
8.
Click “OK”
and Save.
These
steps (1 – 7) create your Stata dataset (that is, .dta file)
ATTENTION: If you are using Stata, make
sure you create a log file and a do-file.
To
create a log file:
The log file gives a history of what you have done.
You can always revisit the log file (saved
as .smcl) to review the processes. So, it is advantageous to always have a
log file. To create a log file:
1.
Go to Stata
>> File >> Log >> Begin
2.
Give it a filename
3.
Click Save
To
create a do-file:
The do-file on the other-hand shows the commands
(codes) used to execute each process. Those familiar with the coding approach
will agree with me that having a do-file can speed up the time used in
executing the work. To create a do-file (saved
as .do):
1.
Go to Stata
>> New Do-File Editor
2.
New do-file opens
3.
Click File >> Save As
4.
Give it a filename
5.
Click Save
Having
established that both explanatory variables are categorical variables
made up of two and four groups respectively, it is important that Value Labels for both explanatory
variables “state” and “chain” are created in Stata. The essence
is to create values for each group in
order to make estimations possible. So, the values for New Jersey and Penn under
state will be 1 and 2 respectively
while those for BK, KFC, RR
and WD under chain will be 1, 2, 3
and 4 respectively.
How to do
that? Here are the steps:
1.
Go to Stata
>> Data >> Data Utilities >> Label
Utilities >> Manage Value Labels >> Create Label
2.
Enter “new
label name”: state
3.
Enter the appropriate values. Enter 1 for Value, and New Jersey for
Label, click ADD. Next, enter 2 for Value, and Penn for Label click ADD. Then click OK.
4.
Again, click “Create
Label”
5.
Enter “new
label name”: chain
6.
Enter the appropriate values. Enter 1 for Value, and BK for Label, click ADD. Next, enter 2 for Value, and KFC for Label click ADD. Again, enter 3 for Value, and RR for Label, click ADD.
Lastly, enter 4 for Value, and WD for Label click ADD. Then click OK.
If it is correctly
done, then you should have something like this as shown below:
 |
| Creating Value Labels for Categorical Variables Using Stata Source: CrunchEconometrix (Used with written permission from Stata) |
Next is
to assign value label to both categorical/explanatory
variables one at a time. To do that:
1.
Go to Stata
>> Data >> Data Utilities >> Label
Utilities >> Assign Value Label to Variable
2.
Under “Variables”
select state
3.
Under “Value
label” select state
4.
Click OK.
5.
Again, under “Variables”
select chain
6.
Under “Value
label” select chain
7.
Click OK.
You
should have something like this for both state
and chain:
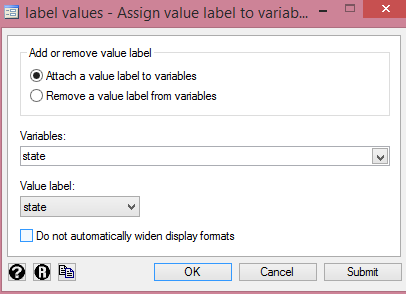 |
| Adding Value Labels to Categorical Variables Source: CrunchEconometrix (Used with written permission from Stata) |
With all
the steps correctly done, your dataset should look like this:
 |
| Dataset showing dependent and explanatory variables in Stata Source: CrunchEconometrix from Wooldridge Dataset (Used with written permission from Stata) |
There are 410 observations, and to know the
distribution of the four fast-food chains across the two states, use the tabulate
syntax. That is,
tab state chain
and you have this output shown below:
 |
| Table showing the distribution of fast-food chains across state Source: CrunchEconometrix from Wooldridge Dataset (Used with written permission from Stata) |
The above table shows how the 410 observations are
distributed among the four fast-food chains in the two US states. For instance,
Roy Rogers has 82 outlets in New Jersey and 17 in Pennsylvania, Wendy’s has 45
outlets in New Jersey and 15 in Pennsylvania and so on.
We are about to dig in much further…J
Please note that in Stata, you can either use the code (command, syntax) approach or the graphical user interface (GUI). Either approach is fine. If you are familiar with the coding
approach, just go ahead and use it, if otherwise use the GUI (where you just
click the applicable menus).
Having prepared our dataset, now let us run the two-way
ANOVA. This tutorial will in the first part
cover the two-way ANOVA analysis and in the second part the post-hoc checks. I will be using the syntax approach, but will show you later
on how to manoeuvre the GUI interface…..are you ready? On the assumption that
our dataset is in line with the six rules….we begin!
State
the null and alternative hypotheses for the test
H0: the location of state will have no
effect on prices charged for small fries
H0: the type of fast-food chain will
have no effect on prices charged for small fries
H0: state and chain interaction will
have no effect on prices charged for small fries
H1: the null hypotheses is not true
All codes are typed into the Command window, as shown below, and you simply press the ENTER key:
 |
| Command box in Stata Source: CrunchEconometrix (Used with written permission from Stata) |
Two-way
ANOVA Procedure
I
will approach this from two angles.
First,
we may want to know the main effects
of each explanatory variable on the dependent variable, and the syntax is:
anova
y
x1 x2
where
the y
is the dependent variable (pfries)
and x1
is the categorical/explanatory variable state
and x2
is the categorical/explanatory variable chain.
This becomes:
anova pfries state chain
The
Stata output is shown as:
The
Stata output churns out quite a lot of information. For instance, the number of
observations is given as 393 instead of 410. Reason is because 17 observations
have missing values. The F-statistics
and the associated p-values are also
indicated. For the Model, the F-statistic (55.25) and its associated p-value (0.0000) shows that both
categorical variables significantly explain pfries.
For state and chain, their F-statistics
and the associated p-values indicate
that both have individual-significant effects on pfries. The R2
(0.3629) shows the percentage of variation in pfries that is explained by state
and chain.
Second,
to obtain both the individual and interactive effects of state and chain on pfries, the syntax is:
anova pfries state chain state#chain
and
the Stata output is as shown below:
 |
| Stata output on the main and explanatory effects Source: CrunchEconometrix |
The
explanations are similar to those stated previously except with the addition of
the interaction term state#chain.
Here the F-statistic (0.31) and its
associated p-value (0.8204) shows
that the joint-effect of both categorical variables insignificantly explains pfries. If a statistically significant
interaction is observed, the result can be followed up by determining if there
are any “simple main effects”, and if there are, what these effects are.
Post-hoc tests
The
F-statistic tells us if there is the
need to perform a post-hoc test or not. If the statistic is significant as it
is for state and chain, then some post-hoc tests can be done but where the statistic
is not significant, then there no need to talk about the variable, act as if
the effect is zero as it is in the case if the interaction term state#chain because in actual fact, the
effect on the population is zero.
Bottom line: only discuss the results that are
significant!
Therefore,
since the main effect of each categorical variable is significant, post-hoc
tests can be performed as done if a one-way ANOVA procedure is conducted. In
this example, we use the Scheffe’s test. But this test will be irrelevant for state since we already know that there
are only two means and the F-statistic
has shown that the difference between them is statistically significant.
However, because we have four groups under chain,
the Scheffe’s test will be relevant in pointing out those combinations between
the groups that have significant differential in their mean prices. The test
can be computed using the syntax:
oneway
pfries chain, scheffe
The
Stata output is shown below:
 |
| Scheffe's post-hoc test in Stata Source: CrunchEconometrix |
The
Scheffe multiple comparison test tells us where the differences are between
each pair of means. Also, in a more-than-two group scenario, this test applies
corrections to the reported significance levels that take into account the fact
that multiple comparisons are being conducted. Thus, as can be seen from the
printout, the difference between the means of BK and KFC is -.053457
and the t-statistic is significant at
the 1% level. With all six combinations, only the difference between WD and KFC (.012284) falls just short of being statistically significant.
Addendum:
By way of information,
here is how to manoeuvre the graphical user interface (GUI) to run the two-way
ANOVA.
Go to Stata >> Statistics >> Linear
models and related >> ANOVA/MANOVA
>> Analysis of variance and
covariance from the top menu, as shown below.
 |
| Graphical user interface (GUI) for Two-way ANOVA in Stata Source: CrunchEconometrix (Used with written permission from Stata) |
A dialogue box for anova - Analysis of variance
and covariance opens:
1.
Under Dependent variable, select pfries from
the drop-down menu
You should have something like this:
 |
| Dialog box for dependent variable in Two-way ANOVA, Stata Source: CrunchEconometrix (Used with written permission from Stata) |
To analyse the individual
effects of both categorical variables on the dependent variables, here is
what to do:
2.
Click
on the three dot button,
, to the far right of the Model: drop-down box and another dialog box
opens where you have Create
varlist with factor variables dialogue box:
·
Under Type of variable, leave Factor variable unchanged
·
Under Specification, leave Main effects unchanged
·
Open the drop
down menu under Variable 1 >> select state >> Add to
varlist
·
Again, open
the drop down menu under Variable 1
>> select chain >> Add to varlist
Both state
and chain will be shown under Varlist, so you should have something
like this:
 |
| Dialog box for factor variables in Two-way ANOVA, Stata Source: CrunchEconometrix (Used with written permission from Stata) |
3.
Click OK and the previous page is modified as
shown below with state and chain appearing under Model:
4.
Click OK to obtain the same regression
outputs as in using the syntax approach.
To analyse the interactive
effects of both categorical
variables on the dependent variables, here is what to do:
1.
Click
on the three dot button,
, to the far right of the Model: drop-down box and another dialog box
opens where you have Create
varlist with factor variables dialogue box:
·
Under Type of variable, leave Factor variable unchanged
·
Under Specification, select Interaction (2-way)
·
Open the drop
down menu under Variable 1 >> select state
·
Open the drop
down menu under Variable 1 >> select chain >> Add to
varlist
2.
Click OK.
If it’s correctly done, state chain state#chain will show under Varlist,
so you have something like this:
 |
| Dialog box for factor and interaction variables in Two-way ANOVA, Stata Source: CrunchEconometrix (Used with written permission from Stata) |
3.
Click OK and you will obtain the same regression
outputs as in using the syntax approach.
Summary of points to note when
running a two-way ANOVA:
1.
Inform
readers about the nature of your study (tell us what you are about to do)
2.
Ensure that
your dependent variable is a continuous value
3.
The
explanatory variables must be categorical variables with at least two groups
4.
Members in
each group must not over-lap
5.
State the
null and alternative hypotheses.
6.
Run the two-way
ANOVA before carrying out any post-hoc checks otherwise Stata will give an
error message.
7.
Report the F-statistic,
degrees of freedom (df), the level of significance (the prob value [Prob>F])
8.
A statement of whether there were statistically
significant differences between your groups and on the interaction term. Report
that of the interaction first if it is significant.
9.
Report the results from the post-hoc
checks and their prob values.
ASSIGNMENT
Using
Wooldridge’s discrim2.dta or discrim2.xlsx show if the price of fries (pfries2) differ among the four
food-chains (Burger King, Kentucky Fried Chicken, Roy Rogers and Wendy’s) across
the two states – New Jersey and Pennsylvania.

