After
unit root testing, what next?
The outcome of
unit root testing matters for the empirical model to be estimated. The
following scenarios explain the implications of unit root testing for further
analysis. Still drawing on the previous tutorials
(see here for EViews, Stata and Excel) on unit root testing with the augmented
Dickey-Fuller procedure (see videos), we are using the same data from Gujarati and Porter Table 21.1 quarterly data of 1970q1 to 1991q4. The variables in
question are pce, pdi and gdp in natural logarithms.
Scenario
1: When series under scrutiny are
stationary in levels.
In this scenario, it is assumed that lnpce, lnpdi and lngdp are
stationary in levels, that is, they are I(0)
series (integrated of order zero). In
this situation, performing a cointegration test is not
necessary. This is because any shock to the system in the short run quickly
adjusts to the long-run. Consequently, only the long
run model should be estimated using OLS (where variables are neither
lagged nor differenced). It is the static form of the model. In essence, the
estimation of short run model is not necessary if series are I(0).
Scenario
2: When series are stationary in first differences.
1.
Under this scenario, the series are
assumed to be non-stationary but became stationary after first difference
2.
One special feature of this is that they
are of the same order of integration.
3. Under this scenario, the model in
question is not entirely useless although the variables are unpredictable. To
verify further the relevance of the model, there is need to test for cointegration. That is, can we assume a long run
relationship in the model despite the fact that the series are drifting apart
or trending either upward or downward?
4. There are however, two prominent
cointegration tests for I(I) series
in the literature. They are Engle-Granger cointegration test and Johansen
Cointegration test.
5. The Engle-Granger test is meant for
single equation model while Johansen cointegration test is considered when
dealing with multiple equations.
If there is cointegration:
1.
Implies that the series in question are
related and therefore can be combined in a linear fashion.
2. That is, even if there are shocks in the
short run, which may affect movement in the individual series, they would
converge with time (in the long run).
3.
Estimate both long-run and short-run
models.
4. The estimation will require the use of
vector autoregressive (VAR) model and vector error correction model (VECM)
analysis.
If
there is no cointegration:
1.
Estimate only the short-run model, which
is VAR and not VECM.
Johansen
Cointegration Test in EViews
The hypothesis
is stated as:
H0:
no cointegrating equation
H1: H0
is not true
Rejection of the null hypothesis is at the 5% level.
Note: Cointegration test should be performed on the level
form of the variables and not on their first difference. It is okay to also use
the log-transformation of the raw variables, as I have done in this example.
Steps:
1.
Load data into EViews (see video on how
to do this)
2.
Open as Group data (see video on how to
do this)
3.
Go to Quick >> Group Statistics >> Johansen Cointegration
>> dialog box opens >> list the variables >> Click OK
>> Select option 3 [Intercept (no trend)] >> Click OK
Here is the
EViews result on the Johansen Cointegration test of lnpce, lnpdi and lngdp:
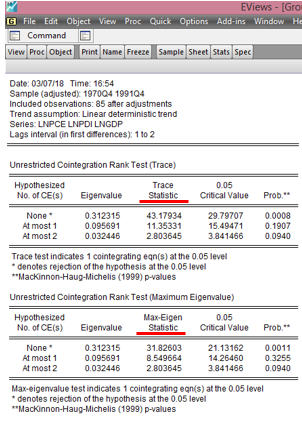 |
| EViews - Johansen Cointegration Test Source: CrucnhEconometrix |
Interpreting
Johansen Cointegration Test Results
1.
The EViews output releases two
statistics, Trace Statistic and Max-Eigen Statistic
2.
Rejection criteria is at 0.05 level
3.
Rejection of the null hypothesis is
indicated by an asterisk sign (*)
4.
Reject the null hypothesis if the
probability value is less than or equal to 0.05
5.
Reject the null hypothesis if the Trace
or Max-Eigen statistic is higher than the 0.05 critical value
Decision: Given the results generated,
the null hypothesis of no cointegrating equation is rejected at the 5% level.
Hence, it is concluded that a long-run relationship exist among the three
variables.
[Watch video on how to conduct Johansen cointegration test in EViews]
However, if the
null hypothesis cannot be rejected, it evidences no cointegration and hence
there is no long-run relationship among the series. This implies that, if there
are shocks to the system, the model is not likely to converge in the long-run. In
addition, if there is no cointegration, only the short run model should be estimated. That is, estimates
only VAR do not estimate a VECM!
