Time Series Analysis (Lecture 4 Part 1): Johansen Cointegration Test in EViews

After unit root testing, what next?

The outcome of unit root testing matters for the empirical model to be estimated. The following scenarios explain the implications of unit root testing for further analysis.  Still drawing on the previous tutorials (see here for EViews, Stata and Excel) on unit root testing with the augmented Dickey-Fuller procedure (see videos), we are using the same data from Gujarati and Porter Table 21.1 quarterly data of 1970q1 to 1991q4. The variables in question are pce, pdi and gdp in natural logarithms.

Scenario 1:  When series under scrutiny are stationary in levels.

In this scenario, it is assumed that lnpce, lnpdi and lngdp are stationary in levels, that is, they are I(0) series (integrated of order zero).  In this situation, performing a cointegration test is not necessary. This is because any shock to the system in the short run quickly adjusts to the long-run. Consequently, only the long run model should be estimated using OLS (where variables are neither lagged nor differenced). It is the static form of the model. In essence, the estimation of short run model is not necessary if series are I(0).  

Scenario 2: When series are stationary in first differences.

1.    Under this scenario, the series are assumed to be non-stationary but became stationary after first difference

2.    One special feature of this is that they are of the same order of integration.

3. Under this scenario, the model in question is not entirely useless although the variables are unpredictable. To verify further the relevance of the model, there is need to test for cointegration.  That is, can we assume a long run relationship in the model despite the fact that the series are drifting apart or trending either upward or downward?

4. There are however, two prominent cointegration tests for I(I) series in the literature. They are Engle-Granger cointegration test and Johansen Cointegration test.

5. The Engle-Granger test is meant for single equation model while Johansen cointegration test is considered when dealing with multiple equations.

If there is cointegration:

1.    Implies that the series in question are related and therefore can be combined in a linear fashion.

2.  That is, even if there are shocks in the short run, which may affect movement in the individual series, they would converge with time (in the long run).

3.    Estimate both long-run and short-run models.

4. The estimation will require the use of vector autoregressive (VAR) model and vector error correction model (VECM) analysis.

If there is no cointegration:

1.    Estimate only the short-run model, which is VAR and not VECM.

Johansen Cointegration Test in EViews

The hypothesis is stated as:

H₀: no cointegrating equation

H₁: H₀ is not true

Rejection of the null hypothesis is at the 5% level.

Note: Cointegration test should be performed on the level form of the variables and not on their first difference. It is okay to also use the log-transformation of the raw variables, as I have done in this example.

Steps:

1.   Load data into EViews (see video on how to do this)

2.   Open as Group data (see video on how to do this)

3.   Go to Quick >> Group Statistics >> Johansen Cointegration >> dialog box opens >> list the variables >> Click OK >> Select option 3 [Intercept (no trend)] >> Click OK

Here is the EViews result on the Johansen Cointegration test of lnpce, lnpdi and lngdp:

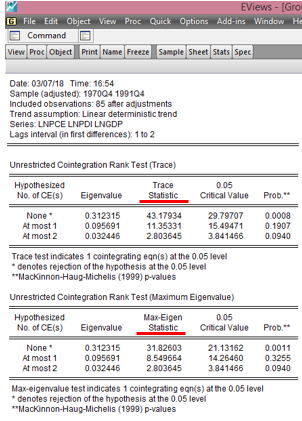EViews - Johansen Cointegration Test
Source: CrucnhEconometrix

Interpreting Johansen Cointegration Test Results

1.   The EViews output releases two statistics, Trace Statistic and Max-Eigen Statistic

2.   Rejection criteria is at 0.05 level

3.   Rejection of the null hypothesis is indicated by an asterisk sign (*)

4.   Reject the null hypothesis if the probability value is less than or equal to 0.05

5.   Reject the null hypothesis if the Trace or Max-Eigen statistic is higher than the 0.05 critical value

Decision: Given the results generated, the null hypothesis of no cointegrating equation is rejected at the 5% level. Hence, it is concluded that a long-run relationship exist among the three variables.

 [Watch video on how to conduct Johansen cointegration test in EViews]

However, if the null hypothesis cannot be rejected, it evidences no cointegration and hence there is no long-run relationship among the series. This implies that, if there are shocks to the system, the model is not likely to converge in the long-run. In addition, if there is no cointegration, only the short run model should be estimated. That is, estimates only VAR do not estimate a VECM!

If there are comments or areas requiring further clarification, kindly post them below….