Interpreting Regression Output from EViews

The dissertation semester is here for undergraduate students in most tertiary institutions, at least for those whose academic calendar is uninterrupted J. The students are in different stages of their project, as it is commonly called. Some are yet to wrap up their chapter one which gives the “study background” and the framing of research hypotheses, objectives and questions. Some have moved on to chapter two reviewing relevant literature related to their scope of study. Others have gone further in developing both the theoretical and empirical frameworks for chapter three, but not without the usual teething lags…but they’ll get around it, somehow J. A handful have made tremendous progress in hitting chapter four attempting to analyse their data.

Because chapters one to three are relative to each students’ scope of work, while a regression output is common to all (although actual outcomes differ), I decided to do this tutorial in explaining the basic features of a regression output. Again, this write-up is in response to requests received from readers on (1) what some specific figures in a regression output are and (2) how to interpret the results. Let me state here that regardless of the analytical software whether Stata, EViews, SPSS, R, Python, Excel etc. what you obtain in a regression output is common to all analytical packages (howbeit with slight changes).

For instance, in undertaking an ordinary least squares (OLS) estimation using any of these applications, the regression output will give the ANOVA (analysis of variance) table, F-statistic, R-squared, prob-values, coefficient, standard error, t-statistic, sum of squared residuals and so on. These are some common features of a regression output. However, the issue is: what do they mean and how can they be interpreted in relation to your study?

Hence, the essence of this tutorial is to teach students the significance of these features and how to interpret their results. I will be using EViews analytical package to explain a regression output, but you can practise along using any analytical package of your choice. (See "How-to-interpret regression output" here for Stata and Excel users).

An Example: Use Gujarati and Porter Table7_12.xlsx dataset

Note: I will not be discussing stationarity or cointegration analysis in this contest, just doing a simple linear regression analysis (a bi-variate analysis) with only one explanatory variable.

The dataset is on the United States from 1960 to 2009 (50 years data). The outcome variable is consumption expenditure (pce) and the explanatory variable is income (income).

First step: Load data in Excel format into EViews

Here is the data in excel format:

Data in Excel file format
Source: CrunchEconometrix

To import the Excel file into EViews, go to: File >> Import >> Import from file >> Next >> Finish. If it is correctly done, you obtain:

Import Excel file into EViews
Source: CrunchEconometrix

Note: In EViews almost everything can be done either by typing commands or by choosing a menu

item (the Guide User Interface, GUI). The choice is a matter of personal preference.

Second step: Visualise the relationship between the variables

Before analysing the data, it is good to always graph the dependent and key explanatory variable (using a scatter plot) in order to observe the pattern between them. It sorts of gives you what to expect in your actual analysis.

Since we want to see the relationship between pce and income over the 50-year period, it means that we want to look at the variables pce and income together. In EViews a collection of series dealt with together is called a Group. Thus, to create a group including pce and income, first click on income. Now, while holding down the Ctrl-key, click on pce. Then right-click anywhere on the interface highlighting New Object, bringing up the context menu as shown below: 

Creating Group data in EViews
Source: CrunchEconometrix

Click New Object and the dialogue box opens:

EViews: New Object dialogue box
Source: CrunchEconometrix

Click OK to open the Series List dialogue box and type in income pce:

EViews: Series List dialogue box
Source: CrunchEconomterix

 Click OK and your data should look like this:

EViews: Group data
Source: CrunchEconometrix

 At this point it is important to save your data file. Click on Name and under Name to identify object change group01 to the desired the file name:

EViews: Object Name dialogue box
Source: CrunchEconometrix

Note: Spaces are not allowed when naming an object in EViews.

I will save this file as pce_income. Click OK and the file appears as G pce_income like this:

EViews: Naming a file
Source: CrunchEconometrix

Now we have finished with all the data prepping. It’s time to observe the relationship between two series. To do that, we will use the scatter diagram. Click on G pce_income to open the file. Then click on View >> Graph >> Scatter >> OK

The scatter diagram indicates a positive relationship between the two variables:

EViews: Scatter plot (pce and income)
Source: CrunchEconometrix

This positive relationship seems plausible because the more income you have, the more you’ll want to consume, except you are very economical J.

To graph the model (pce) with the linear prediction (pce_hat), Click on G pce_income to open the file. Then click on View >> Graph >> Scatter >> on the left-hand side of the dialog that pops up >> select Regression line from the Fit lines dropdown menu. The default options for a regression line are fine, so hit to dismiss the dialog.

Or, simply right click inside the graph: Fit lines >> select Regression line >> OK

EViews: Scatter plot with fit line
Source: CrunchEconometrix

As observed from the graph, all the points do not fall on the predicted line. Some lie above, while some are beneath the line. These are all the residuals (in order words, the remnants obtained after the regression analysis).

Third step: The scientific investigation

Now we want to scientifically investigate the relationship between pce and income. In EViews you specify a regression with the ls command followed by a list of variables. (“LS” is the name for the EViews command to estimate an ordinary Least Squares regression.) The first variable is the dependent variable, the variable we’d like to explain pce in this case. The rest of the list gives the independent variables, which are used to predict the dependent variable.

Also, one can “run a regression” either by using the menu or type-command approach. Using the menu approach, from the Tool Bar, pick the menu item Quick >> Estimate Equation and a dialog box opens:

 

EViews: Equation Estimation dialogue box
Source: CrunchEconometrix

Under Equation specification, type “pce c income” click OK.

Hold on a bit. If pce is the dependent variable and income is the explanatory variable so, where does the “C” in the command come from? “C” is a special keyword telling EViews to estimate the equation with an intercept.

And if you prefer to use the type-command approach, go to the command section and type in:

ls pce c income

(You have simply told EViews to regress the dependent variable, pce, on the explanatory variable, income and a constant).

Therefore, whether you use the menu or type a command, EViews churns out the regression results shown below:

EViews: Regression Output
Source: CrunchEconometrix

Fourth step: The features of a regression output

So what do these figures mean? I will explain each feature in turns.

Dependent variable: this is pce and it is clearly defined. It is also the outcome variable.

Method: this is the estimation technique. In this example, it is ordinary least squares

Date: captures the exact time you are carrying out the analysis

Sample: must be in line with your scope of research; that is 1960 to 2009

Included observations: since the data span is from 1960 to 2009, observations = 50

Variable: includes both the intercept and slope

Coeff: these captures the estimates for intercept and slope. The sign of the coefficient also tells the direction of the relationship. A positive (negative) sign implies a positive (negative) relationship.

Std. error: this is the standard deviation for the coefficient. That is, since you are not so sure about the exact value for income, there will be some variation in the prediction for the coefficient. Therefore, the standard error shows how much deviation occurs from predicting the slope coefficient estimate.

t-stat: this measures the number of standard errors that the coefficient is from zero. It is obtained by: coefficient/std.error. A t-stat above 2 is sufficient evidence against the null hypothesis

Prob.: there are several interpretations for this. (1) it is smallest evidence required to reject the null hypothesis, (2) it is the probability that one would have obtained the slope coefficient value from the data if the actual slope coefficient is zero, (3) the p-value looks up the t-stat table using the degree of freedom (df) to show the number of standard errors the coefficient is from zero, (4) tells whether the relationship is significant or not.

So, if the p-value is 0.35, then it means that you are only 65% (that is, (100-35)%) confident that the slope coefficient is non-zero. This is not good enough. This is because a very low p-value gives a higher level of confidence in rejecting the null hypothesis. Hence, a p-value of 0.01, implies that you are 99% (that is, (100 - 1)%) confident that the slope coefficient is non-zero. This is very comforting! J.

R-squared: the value of 0.999273 gives the variation in pce that is explained by income. The higher the R², the better the model and the more predictive power the variables have. Although, an R² that equals 1 will elicit some suspicion. The R is actually the correlation coefficient between the 2 variables. That implies that:   

 

= the correlation coefficient.

Adjusted R-squared: this is the R² adjusted as you increase your explanatory variables. It (0.999257) reduces as more explanatory variables are added.

S.E of regression: this is the summary measure based on the estimated variance of the residuals.

Sum squared resid: implies sum of squared residuals for the Model (explained variation in pce) and Residuals (unexplained variation in pce). After doing the regression analysis, all the points on pce_hat do not fall on the regression line. Those points outside the line are known as residuals. Those that can be explained by the model are known as Explained Sum of Squares (ESS) while those that are due to random nature, which are outside the model are known as Residual Sum of Squares (RSS).

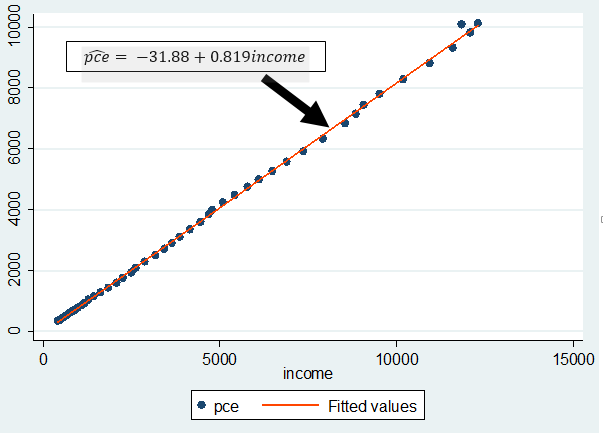
Having seen the plot of the scatter diagram, it is pretty clear that the predicted line does an almost-accurate job of giving a 50-year summary of pce. In regression analysis, the amount by which the right-hand side of the equation misses the dependent variable is called the residual. Calling the residual e (“e” stands for “error”), we can write an equation that really is valid in each and every year, that is: pce = -31.88 + 0.819income + e

Since the residual is the part of the equation that’s left over after we’ve explained as much as possible with the right-hand side variables, one approach to getting a better fitting equation is to look for patterns in the residuals.

To obtain the table showing the predicted and residual values, go to View >> Actual, Fitted, Residual >> Actual, Fitted, Residual Table and you get:

EViews: Table of actual, predicted and residual values
Source: CrunchEconometrix

If the predicted line falls above a point, it means that pce is over-predicted (that is, pce – pce_hat is negative) and if it is beneath a point, it implies that pce is under-predicted (that is, pce – pce_hat is positive). The sum and mean of the residuals equals zero.

Likewise, to obtain the plot of the predicted and residual values, go to View >> Actual, Fitted, Residual >> Actual, Fitted, Residual Graph and you get:

EViews: Graph of actual, predicted and residual values
Source: CrunchEconometrix

Log likelihood: this the difference between the log likelihood values of the restricted and unrestricted versions of the model.

F-statistic: captures whether the explanatory variable, income is significant in explaining the outcome variable, pce. The higher the F-stat, the better for the model.

Prob (F-statistic): the probability value of 0.0000 is the probability value that indicates the statistical significance of the F statistic. You will prefer to have a prob-value that is less than 0.05.

Mean dependent var: the figure of 3522.160 indicates the average value of pce in the data.

S. D. dependent var: the figure of 3077.678 indicates the deviation from the average value of pce in the data

Akaike/Schwartz/Hannan-Quinn info criterion: these are often used to choose between competing models. The lower the value of these criteria, the better the model is. From this example, the Akaike info criterion (AIC) figure of 11.73551 is the lowest of the three and therefore indicates that it is the best model to adopt in this case.

Durbin-Watson stat: is used to find out if there is first-order serial correlation in the error terms. Rule of thumb: if DW < 2 equals evidence of positive serial correlation. So, from our example, the DW value of 0.568044 indicates serial correlation in the residuals.

Assignment:

Use Gujarati and Porter Table7_12.xlsx dataset.

(1)  With pce as the dependent variable and gdpi as the explanatory variable, plot the graph of pce and gdpi, what do you observe?

(2)  Run your regression. Can you interpret the table and the features?

(3)  Plot the predicted line. What are your observations?

[Watch video on how to interpret regression output in EViews]

I have taken you through the basic features of a regression output using EViews analytical package on ordinary least squares (OLS) model in a simple linear regression. Practice the assignment and if you still have further questions, kindly post them below…..

How to Interpret Regression Output in Stata

How to Interpret Regression Output in Stata

This period happens to be the dissertation semester for undergraduate students in most universities, at least for those with undisrupted academic calendar J. The students are in different stages of their project, as it is commonly called. Some are yet to wrap up their chapter one which gives the “study background” and the framing of research hypotheses, objectives and questions. Some have moved on to chapter two reviewing relevant literature related to their scope of study. Others have gone further in developing both the theoretical and empirical frameworks for chapter three, but not without the usual teething lags…but they’ll get around it, somehow J. A handful have even done better by progressing to chapter four attempting to analyse their data.

Since, chapters one to three are relative to each students’ scope of research, but a regression output is common to all (although actual outcomes differ), I decided to do this tutorial in explaining the basic features of a regression output. Also, this write-up is in response to requests received from readers on (1) what some specific figures in a regression output are and (2) how to interpret the results. Let me state here that regardless of the analytical software whether Stata, EViews, SPSS, R, Python, Excel etc. what you obtain in a regression output is common to all analytical packages.

For instance, in undertaking an ordinary least squares (OLS) estimation using any of these applications, the regression output will churn out the ANOVA (analysis of variance) table, F-statistic, R-squared, prob-values, coefficient, standard error, t-statistic, degree of freedom, 95% confidence interval and so on. These are the basic features of a regression output regardless of your model and/or estimation technique. However, the issue is: what do they mean and how can they be interpreted and related to your study.

Hence, the essence of this tutorial is to teach students the relevance of these features and how to interpret their results. I will be using Stata analytical package to explain a regression output, but you can practise along using any analytical package of your choice. (See "How-to-interpret regression output" here for EViews and Excel users)

An Example: Using Gujarati and Porter Dataset Table7_12.dta or Table7_12.xlsx dataset

Note: In this tutorial I will not be discussing stationarity or cointegration analysis (those topics will be covered in subsequent tutorials). Since the purpose is simply to explain the basic features of a regression output, I will only be doing a simple linear regression analysis (a bi-variate analysis) with only one explanatory variable.

The dataset is on the United States from 1960 to 2009 (50 years data). The outcome variable is consumption expenditure (pce) and the explanatory variable is income (income).

First step: load data in excel format into Stata

Here is the data in excel format:

Data in Excel format
Source: CrunchEconometrix

And here is the data in Stata format:

Data in Stata format
Source: CrunchEconometrix

Second step: Set the time variable in Stata for analysis

Before analysing the data, you must set up the time variable in readiness for the regression. The general code is:

tsset timevar

in my case, the time variable is obs, and my code becomes:

tsset obs

and Stata responds with:

Time set command in Stata
Source: CrunchEconometrix

The tsset implies “time series set” and as you can see, the begin year is 1960 and the end year is 2009. You must always do this after loading your data and before you begin your regressions.

Third step: Visualise the relationship between the variables

Before analysing the data, it is good to always graph the dependent and key explanatory variable (using a scatter plot) in order to observe the pattern between them. It kind of gives you what to expect in your actual analysis.

So, to graph pce and income, the Stata code is:

twoway (scatter pce income)

The scatter diagram indicates a positive relationship between the two variables:

Scatter plot of the variables
Source: CrunchEconomterix

This positive relationship seems plausible because the more income you have, the more you’ll want to consume, except you are very frugal J.

Fourth step: The scientific investigation

Now we want to scientifically investigate the relationship between pce and income. The Stata code is:

regress pce income

(You have simply told Stata to regress the dependent variable, pce, on the explanatory variable, income), and the output is shown as:

Regression output in Stata
Source: CrunchEconometrix

Fifth step: The features of a regression output

So what do these figures mean? I will explain each feature in turns.

Source: there are two sources of variation in the dependent variable, pce. Those explained by the regression (i.e, the Model) and those due to randomness (Residuals)

SS: implies sum of squared residuals for the Model (explained variation in pce) and Residuals (unexplained variation in pce). After doing the regression analysis, all the points on pce_hat do not fall on the regression line. Those points outside the line are known as residuals. Those that can be explained by the model are known as Explained Sum of Squares (ESS) while those that are due to random nature, which are outside the model are known as Residual Sum of Squares (RSS).

To graph the model (pce) with the linear prediction (pce_hat), the Stata code is:

scatter pce income || lfit pce income

 

Scatter plot of the linear prediction
Source: CrunchEconometrix

As observed from the graph, all the points do not fall on the predicted line. Some lie above, while some are beneath the line. These are all the residuals (in order words, the remnants obtained after the regression analysis).

To obtain the predicted value, the Stata command is:

predict pce_hat

and to obtain the residual value, the Stata command is:

predict pce_resid

Predicted and residual value of the dependent variable
Source: CrunchEconometrix

If the predicted line falls above a point, it means that pce is over-predicted (that is, pce – pce_hat is negative) and if it is beneath a point, it implies that pce is under-predicted (that is, pce – pce_hat is positive). The sum and mean of the residuals equals zero.

df: this is degree of freedom calculated as k - 1 (for the model) and n - k (for the residuals). n = number of observations; k = number of restrictions on the model

MS: implies mean sum of squared residuals and obtained by dividing SS by df i.e. SS/df

No. of obs: the data span is from 1960 to 2009 = 50 years

F-stat: captures whether the explanatory variable, income is significant in explaining the outcome variable, pce. The higher the F-stat, the better for the model.

Prob>F: this is the probability value that indicates the statistical significance of the F ratio.You will prefer to have a prob-value that is less than 0.05.

R-squared: gives the variation in pce that is explained by income. The higher the R², the better the model and the more predictive power the variables have. Although, an R² that equals 1 will elicit some suspicion. The R is actually the correlation coefficient between the 2 variables. This implies that: 

= the correlation coefficient.

Adjusted R-squared: this is the R² adjusted as you increase your explanatory variables. It reduces as more explanatory variables are added.

Coeff: this is the slope coefficient. The estimate for income. The sign of the coefficient also tells you the direction of the relationship. A positive (negative) sign implies a positive (negative) relationship.

_cons: this is the hypothetical outcome on pce if income is zero. It is also the intercept for the model.

Std. error: this is the standard deviation for the coefficient. That is, since you are not so sure about the exact value for income, there will be some variation in the prediction for the coefficient. Therefore, the standard error shows how much deviation occurs from predicting the slope coefficient estimate.

t-stat: this measures the number of standard errors that the coefficient is from zero. It is obtained by:  coeff/std. error. A t-stat above 2 is sufficient evidence against the null hypothesis

P>|t|: there are several interpretations for this. (1) it is smallest evidence required to reject the null hypothesis, (2) it is the probability that one would have obtained the slope coefficient value from the data if the actual slope coefficient is zero, (3) the p-value looks up the t-stat table using the degree of freedom (df) to show the number of standard errors the coefficient is from zero, (4) tells whether the relationship is significant or not.

So, if the p-value is 0.4, then it means that you are only 60% (that is, (100-40)% ) confident that the slope coefficient is non-zero. This is not good enough. This is because a very low p-value gives a higher level of confidence in rejecting the null hypothesis. Hence, a p-value of 0.02, implies that you are 98% (that is, (100 - 2)% ) confident that the slope coefficient is non-zero. This is very comforting! J.

95% confidence interval: if the coefficient is significant, this interval will contain that slope coefficient but it will not, if otherwise.

Assignment:

Use Gujarati and Porter datasets Table7_12.dta or Table7_12.xlsx dataset.

(1)  With pce as the dependent variable and gdpi as the explanatory variable, plot the graph of pce and gdpi, what do you observe?

(2)  Run your regression. Can you interpret the table and the features?

(3)  Plot the predicted line. What are your observations?

I have taken you through the basic features of a regression output using Stata analytical software on ordinary least squares (OLS) model in a simple linear regression. Hence, you now have the basic idea of what the F-stat, t-stat, df, SS, MS, prob>F, p>|t|, confidence interval, R², coefficient, standard error stand for.

Practice the assignment and if you still have further questions, kindly post them below…..