How to Interpret Regression Output in Stata
This period happens to be the dissertation semester for undergraduate
students in most universities, at least for those with undisrupted academic
calendar J. The students
are in different stages of their project,
as it is commonly called. Some are yet to wrap up their chapter one which gives
the “study background” and the framing of research hypotheses, objectives and
questions. Some have moved on to chapter two reviewing relevant literature
related to their scope of study. Others have gone further in developing both
the theoretical and empirical frameworks for chapter three, but not without the
usual teething lags…but they’ll get around it, somehow J. A handful have even done better
by progressing to chapter four attempting to analyse their data.
Since, chapters one to three are
relative to each students’ scope of research, but a regression output is common
to all (although actual outcomes differ), I decided to do this tutorial in
explaining the basic features of a regression output. Also, this write-up is in
response to requests received from readers on (1) what some specific figures in
a regression output are and (2) how to interpret the results. Let me state here
that regardless of the analytical software whether Stata, EViews, SPSS, R,
Python, Excel etc. what you obtain in a regression output is common to all
analytical packages.
For instance, in undertaking an ordinary
least squares (OLS) estimation using any of these applications, the regression
output will churn out the ANOVA (analysis of variance) table, F-statistic, R-squared, prob-values, coefficient, standard error, t-statistic, degree of freedom, 95%
confidence interval and so on. These are the basic features of a regression output regardless of your model and/or estimation technique. However,
the issue is: what do they mean and how can they be interpreted and related to
your study.
Hence, the essence of this tutorial is to
teach students the relevance of these features and how to interpret their
results. I will be using Stata
analytical package to explain a regression output, but you can practise along
using any analytical package of your choice.
An Example: Using Gujarati and Porter Dataset Table7_12.dta
or Table7_12.xlsx dataset
Note: In this tutorial I will not be discussing
stationarity or cointegration analysis (those topics will be covered in subsequent tutorials). Since the purpose is simply to explain the basic features of a regression output, I will only be doing a simple linear regression
analysis (a bi-variate analysis) with only one explanatory variable.
The dataset is on the United States from
1960 to 2009 (50 years data). The outcome variable is consumption expenditure (pce) and the explanatory variable is
income (income).
First step: load data in excel format into Stata
Here is the data in excel format:
 |
| Data in Excel format Source: CrunchEconometrix |
And here is the data in Stata format:
 |
| Data in Stata format Source: CrunchEconometrix |
Second step: Set the time variable in Stata for analysis
Before analysing the data, you must set
up the time variable in readiness for the regression. The general code is:
tsset
timevar
in my case, the time variable is obs, and my code becomes:
tsset
obs
and Stata responds with:
 |
| Time set command in Stata Source: CrunchEconometrix |
The tsset
implies “time series set” and as you
can see, the begin year is 1960 and the end year is 2009. You must always do
this after loading your data and before you begin your regressions.
Third step: Visualise the relationship between the variables
Before analysing the data, it is good to
always graph the dependent and key explanatory variable (using a scatter plot) in
order to observe the pattern between them. It kind of gives you what to expect
in your actual analysis.
So, to graph pce and income, the Stata
code is:
twoway
(scatter pce income)
The scatter diagram
indicates a positive relationship between the two variables:
 |
| Scatter plot of the variables Source: CrunchEconomterix |
This positive relationship seems
plausible because the more income you have, the more you’ll want to consume, except
you are very frugal J.
Fourth step: The scientific investigation
Now we want to scientifically
investigate the relationship between pce
and income. The Stata code is:
regress
pce income
(You have simply told Stata to regress
the dependent variable, pce, on the
explanatory variable, income), and
the output is shown as:
 |
| Regression output in Stata Source: CrunchEconometrix |
Fifth step: The features of a regression output
So what do these figures mean? I will
explain each feature in turns.
Source: there are two
sources of variation in the dependent variable, pce. Those explained by the regression (i.e, the Model)
and those due to randomness (Residuals)
SS: implies sum of squared residuals for the Model (explained
variation in pce) and Residuals
(unexplained variation in pce). After
doing the regression analysis, all the points on pcehat do not fall on the regression line.
Those points outside the line are known as residuals. Those that can be
explained by the model are known as Explained
Sum of Squares (ESS) while those that are due to random nature, which are outside
the model are known as Residual Sum of
Squares (RSS).
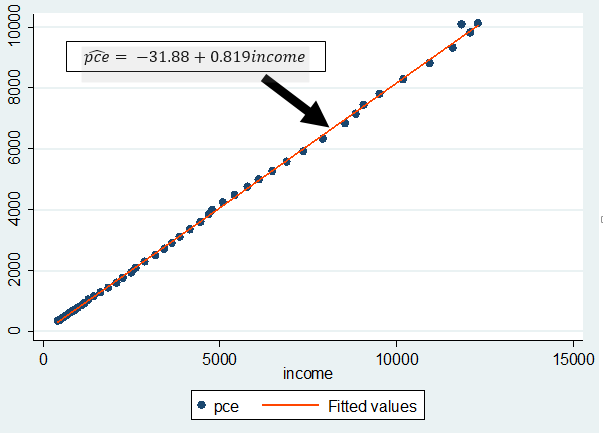
To graph the model (pce) with the linear prediction (pcehat), the Stata code is:
scatter
pce income || lfit pce income
As observed from the graph, all the
points do not fall on the predicted line. Some lie above, while some are
beneath the line. These are all the residuals (in order words, the remnants obtained
after the regression analysis).
To obtain the predicted value, the Stata
command is:
predict pce_hat
and to obtain the residual value, the
Stata command is:
predict pce_resid
 |
| Predicted and residual value of the dependent variable Source: CrunchEconometrix |
If the predicted line falls above a
point, it means that pce is
over-predicted (that is, pce – pcehat
is negative) and if it is beneath a point, it implies that pce is under-predicted (that is, pce – pcehat is positive). The sum and mean of the residuals
equals zero.
df: this is degree of freedom calculated as k - 1 (for the model)
and n - k (for the residuals). n = number of observations; k = number of restrictions on the model
MS: implies mean sum of squared residuals and obtained by dividing SS by df i.e. SS/df
No.
of obs:
the data span is from 1960 to 2009 = 50 years
F-stat: captures
whether the explanatory variable, income
is significant in explaining the outcome variable, pce. The higher the F-stat, the better for the model.
Prob>F: this is the
probability value that indicates the statistical significance of the F ratio.You will prefer to have a prob-value that is less than 0.05.
R-squared: gives the
variation in pce that is explained by
income. The higher the R2, the better the model and
the more predictive power the variables have. Although, an R2 that equals 1 will elicit some suspicion. The R is
actually the correlation coefficient between the 2 variables. This implies that:
= the correlation coefficient.
Adjusted R-squared: this is the R2 adjusted as you increase your explanatory variables.
It reduces as more explanatory variables are added.
Coeff: this is the
slope coefficient. The estimate for income.
The sign of the coefficient also tells you the direction of the relationship. A
positive (negative) sign implies a positive (negative) relationship.
_cons: this is the
hypothetical outcome on pce if income is zero. It is also the intercept
for the model.
Std.
error:
this is the standard deviation for the coefficient. That is, since you are not
so sure about the exact value for income,
there will be some variation in the prediction for the coefficient. Therefore,
the standard error shows how much deviation occurs from predicting the slope
coefficient estimate.
t-stat: this measures
the number of standard errors that the coefficient is from zero. It is obtained
by: coeff/std. error. A t-stat above 2 is sufficient
evidence against the null hypothesis
P>|t|: there are
several interpretations for this. (1) it is smallest evidence required to
reject the null hypothesis, (2) it is the probability that one would have
obtained the slope coefficient value from the data if the actual slope coefficient
is zero, (3) the p-value looks up the t-stat
table using the degree of freedom (df) to show the number of standard errors
the coefficient is from zero, (4) tells whether the relationship is significant
or not.
So, if the p-value is 0.4, then it means that you are only 60% (that is,
(100-40)% ) confident that the slope coefficient is non-zero. This is not good
enough. This is because a very low p-value
gives a higher level of confidence in rejecting the null hypothesis. Hence, a p-value of 0.02, implies that you are
98% (that is, (100 - 2)% ) confident that the slope coefficient is non-zero.
This is very comforting! J.
95%
confidence interval:
if the coefficient is significant, this interval will contain that slope
coefficient but it will not, if otherwise.
Assignment:
Use Gujarati and Porter datasets Table7_12.dta or
Table7_12.xlsx dataset.
(1) With pce
as the dependent variable and gdpi as
the explanatory variable, plot the graph of pce
and gdpi, what do you observe?
(2) Run your regression. Can you interpret the
table and the features?
(3) Plot the predicted line. What are your
observations?
I have taken you through the basic
features of a regression output using Stata analytical software on ordinary
least squares (OLS) model in a simple linear regression. Hence, you now have the
basic idea of what the F-stat, t-stat, df, SS, MS, prob>F, p>|t|,
confidence interval, R2,
coefficient, standard error stand for.
Practice the assignment and if you still
have further questions, kindly post them below…..


No comments:
Post a Comment