Time Series Analysis (Lecture 3): How to Perform Stationarity Test in EViews

How to Perform Unit Root Test in EViews

What is Stationarity in Time Series Analysis?In econometrics, time series data are frequently used and they often pose distinct problems for econometricians. As it will be discussed with examples, most empirical work based on time series data assumes that the underlying series is stationary. Stationarity of a series (that is, a variable) implies that its mean, variance and covariance are constant over time. That is, these do not vary systematically over time. In order words, they are time invariant. However, if that is not the case, then the series is nonstationary. We will discuss some possible scenarios where two series, Y and X, are nonstationary and the error term, u, is also nonstationary. In that case, the error term will exhibit autocorrelation. Another likely scenario is where Y and X are nonstationary, but u is stationary. The implications of this will also be explored. In time series analysis, the words nonstationary, unit root or random walk model are used synonymously. In essence, of a series is considered to be nonstationary, it implies that such exhibit a unit root and exemplifies a random walk series.

Regressing two series that are nonstationary, likewise, yields a spurious (or nonsense) regression. That is, a regression whose outcome cannot be used for inferences or forecasting. In short, such results should not be taken seriously and must be discarded. A stationary series will tend to return to its mean (called mean reversion) and fluctuations around this mean (measured by its variance) will have a broadly constant breadth. But if a time series is not stationary in the sense just explained, it is called a nonstationary time series such will have a time-varying mean or a time-varying variance or both. In summary, a stationary time series is important because if such is nonstationary, its behaviour can be studied only for the time period under consideration. That is, each set of time series data will therefore be for a particular episode. As a result, it is not possible to generalise its relevance to other time periods. Therefore, for the purpose of forecasting, such (nonstationary) time series may be of little practical value

How to detect unit root in a series?

In a bivariate (2 variables) model or that involving multiple variables (called a multiple regression model), it is assumed that all the variables are stationary at level (that is, the order of integration of each of the variable is zero, I(0). It is important to state at this point, that the order of integration of a series in a regression model is determined by the outcome of a unit root test (or stationarity test). If the series is stationary at level after performing unit root test, then it is I(0), otherwise it is I(d) where d represents the number of times the series is differenced before it becomes stationary. But what if the assumption of stationarity at level of the series in a bivariate or multiple regression model is relaxed and we consequently allow for a unit root in each of the variables in the model, how can this be corrected? In general, this would require a different treatment from a conventional regression with stationary variables at I(0).

In particular, we focus on a class of linear combination of unit root processes known as cointegrated process. The generic representation for the order of integration of series is I(d) where d is the number of differencing to render the series stationary. Hence, a stationary series at level, d = 0 is a series with an I(0) process. Although, for any non-stationary series, ‘d’ can assume any value greater than zero, however, in applied research, only the unit root process of I(1) process is allowed, otherwise such series with higher order of integration (d > 1) should be excluded in the model as no meaningful policy implications or relevance can be drawn from such series. 

Here is an example of a bivariate linear regression model:

                                           Y_t = 𝛂₀ + bX_t + u_t                                               [1]

Assume Y_t and X_t  are two random walk models that are I(1) processes and are independently distributed as:   

                       Y_t = ρY_t-1 +  v_t,                     -1 ≤  ρ ≤ 1                                 [2]        

                       X_t = ղX_t-1 +  e_t,                    -1 ≤  ղ ≤ 1                                 [3]

and v_t and e_t have zero mean, a constant variance and are orthogonal (these are white noise error terms). 

We also assumed that v_t and e_t are serially uncorrelated as well as mutually uncorrelated. As stated in [2] and [3], both these time series are nonstationary; that is, they are I(1) or exhibit stochastic trends. Suppose we regress Y_t on X_t. Since Y_t on X_t are uncorrelated I(1) processes, the R² from the regression of Y on X should tend to zero; that is, there should not be any relationship between the two variables. Equations [2] and [3] resemble the Markov first-order autoregressive model. If ρ and ղ = 1, the equations become a random walk model without drift. If ρ and ղ are in fact 1, then a unit root problem surfaces, that is, a situation of nonstationarity; because we already know that in this case the variance of Y_t is not stationary. The name unit root is due to the fact that ρ = 1. Again, the terms nonstationary, random walk, and unit root can be treated as synonymous. If, however, |ρ| ≤ 1, and  |ղ| ≤ 1, that is if their absolute values are less than one, then it can be shown that both series Y_t and X_t are stationary. In practice, then, it is important to find out if a time series possesses a unit root.

Given equations [2] and [3], there should be no systematic relationship between Y_t and X_t as they both drift away from equilibrium (i.e. they do not converge), and therefore, we should expect that an ordinary least squares (OLS) estimate of b should be close to zero, or insignificantly different from zero, at least as the sample size increases. But this is not usually the case. The fitted coefficients in this case may be statistically significant even when there is no true relationship between the dependent variable and the regressors. This is regarded as a spurious regression or correlation where, in the case of our example, b takes any value randomly, and its t-statistic indicates significance of the estimate.

But how can unit root be detected? There are some clues that tell you if a series is nonstationary and if the regression of bivariate or multivariate relationships are spurious. Some of these are:

1.   Do a graphical plot of the series to visualise the nature. Is it trending upwards or downwards? Does it exhibit a mean-reversion or not? Or are there fluctuations around its mean?

2.   Or carry out a regression analysis on two series and observe the R². If it is above 0.9, it may suggest that the variables are nonstationary.

3.    The rule-of-thumb: if the R² obtained from the regression is higher than the Durbin Watson (DW) statistic. The low DW statistic evidences positive first order auto-correlation of the error terms.

Using Gujarati and Porter Table 21.1 quarterly data of 1970q1 to 1991q4, examples of nonstationary series and spurious regression can be seen from the pce, pdi and gdp relationship. Since the series are measured in billions of US dollars, the natural logarithms of the variables will be used in analysing their essential features.

Nonstationary series: the graphical plot of the three variables shows an upward trend and none of the variables revert to their means. That is, all three variables do not exhibit mean reversions. That clearly tells us that the series are nonstationary.

EViews - Example of nonstationary series
Source: CrunchEconometrix

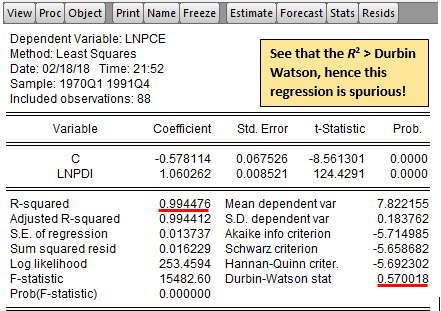
What is a spurious regression? Sometimes we expect to find no relationship between two variables, yet a regression of one on the other variable often shows a significant relationship. This situation exemplifies the problem of spurious, or nonsense, regression. The regression of lnpce on lnpdi shows how spurious regressions can arise if time series are not stationary. As expected, because both variables are nonstationary, the result evidences that a spurious regression has been undertaken.

But how do we know this? Take a look at the R² the value of 0.9944 is higher than the Durbin Watson statistic of 0.57. So, whenever the R² > DW, a spurious regression has occurred because the variables are nonstationary.

EViews - Example of a spurious regression
Source: CrunchEconometrix

As you can see, the coefficient of lnpdi is highly statistically significant, and the R² value is statistically significantly different from zero. From these results, you may be tempted to conclude that there is a significant statistical relationship between both variables, whereas a priori there may or may not be none. This is simply the phenomenon of spurious or nonsense regression, first discovered by Yule (1926). He showed that (spurious) correlation could persist in nonstationary time series even if the sample is very large. That there is something wrong in the preceding regression is suggested by the extremely low Durbin–Watson value, which suggests very strong first-order autocorrelation. According to Granger and Newbold, R² > DW is a good rule of thumb to suspect that the estimated regression is spurious, as in the given example.

Why is it important to test for stationarity?

We usually consider a nonstationary series for the following reasons:

1.    To evaluate the behaviour of series over time. Is the series trending upward or downward? This can be verified from performing a stationarity test. In other words, the test can be used to evaluate the stability or predictability of time series. If a series is nonstationary, that means the series is unstable or unpredictable and therefore may not be valid for inferences, prediction or forecasting.

2.     To know how a series responds to shocks requires carrying out a stationarity test. If such series is nonstationary, the impact of shocks to the series are more likely to be permanent. Consequently, if a series is stationary, impact of shocks will be temporary or brief.

How to correct for nonstationarity?

What can be done with nonstationarity in a time series knowing that performing OLS on such a model yields spurious regression?

The Unit Root Test

We begin with equations [2] and [3] which are unit root (stochastic) processes with white noise error terms. If the parameters of the models are equal to 1, that is, in the case of the unit root, both equations become random walk models without drift, which we know is a nonstationary stochastic process. So, what can be done to correct this? For instance, for equation [2], simply regress Y_t on its (one-period) lagged value Y_t−1 and find out if the estimated ρ is statistically equal to 1? If it is, then Y_t is nonstationary. Repeat same for the X_t series. This is the general idea behind the unit root test of stationarity.

For theoretical reasons, equation [2] is manipulated as follows: Subtract Y_t−1 from both sides of [2] to obtain:

                                           Y_t  - Y_t-1 =  ρY_t-1 - Y_t-1 +  v_t                        [4]

                                                         = (ρ - 1)Y_t-1 +  v_t

                                     

and this can be stated alternatively as:

⃤ Y_t  = δY_t-1 +  v_t                                                [5]

where δ = (ρ − 1) and  ⃤, as usual, is the first-difference operator. In practice, therefore, instead of estimating [2], we estimate [5] and test the null hypothesis that δ = 0. If δ = 0, then ρ = 1, that is we have a unit root, meaning the time series under consideration is nonstationary.

Before we proceed to estimate [5], it may be noted that if δ = 0, [5] will become:

⃤ Y_t  = Y_t-1 - Y_t-1 =  v_t                          [6]

(Remember to do the same for X_t series)

Since v_t is a white noise error term, it is stationary, which means that the first difference of a random walk time series is stationary.

 

EViews - Example of stationary series (in first difference)
Source: CrunchEconometrix

Visual observation of the differenced series shows that the three variables are stationary around the mean. They all exhibit constant mean-reversions. That is, they fluctuate around 0. If we are to draw a trend line, such a line will be horizontal at 0.01.

Okay, having said all that. Let us return to estimating equation [5]. This is quite simple, all that is required is to take the first differences of Y_t and regress on Y_t−1 and see if the estimated slope coefficient in this regression is statistically different from is zero or not. If it is zero, we conclude that Y_t is nonstationary. But if it is negative, we conclude that Y_t is stationary.

Note: Since δ = (ρ − 1), for stationarity ρ must be less than one. For this to happen δ must be negative!

The only question is which test do we use to find out if the estimated coefficient of Y_t−1 in [5] is zero or not? You might be tempted to say, why not use the usual t test? Unfortunately, under the null hypothesis that δ = 0 (i.e., ρ = 1), the t value of the estimated coefficient of Y_t−1 does not follow the t distribution even in large samples; that is, it does not have an asymptotic normal distribution.

What is the alternative? Dickey and Fuller (DF) have shown that under the null hypothesis that δ = 0, the estimated t value of the coefficient of Y_t−1 in [5] follows the τ (tau) statistic. These authors have computed the critical values of the tau statistic on the basis of Monte Carlo simulations.

Note: Interestingly, if the hypothesis that δ = 0 is rejected (i.e., the time series is stationary), we can use the usual (Student’s) t test.

The unit root test can be computed under three (3) different null hypotheses. That is, under different model specifications such as if the series is a:

1.    random walk (that is, model has no constant, no trend)

2.    random walk with drift (that is, model has a constant)

3.    random walk with drift and a trend (that is, model has a constant and trend)

In all cases, the null hypothesis is that δ = 0; that is, there is a unit root and the alternative hypothesis is that δ is less than zero; that is, the time series is stationary. If the null hypothesis is rejected, it means that Y_t is a stationary time series with zero mean in the case of [5], that Y_t is stationary with a nonzero mean in the case of a random walk with drift model, and that Y_t is stationary around a deterministic trend in the case of random walk with drift around a trend.

It is extremely important to note that the critical values of the tau test to test the hypothesis that δ = 0, are different for each of the preceding three specifications of the DF test, which are now computed by all econometric packages. In each case, if the computed absolute value of the tau statistic (|τ|) exceeds the DF or MacKinnon critical tau values, the null hypothesis of a unit root is rejected, in order words the time series is stationary. On the other hand, if the computed |τ| does not exceed the critical tau value, we fail to reject the null hypothesis, in which case the time series is nonstationary.

Note: Students often get confused in interpreting the outcome of a unit root test. For instance, if the calculated tau statistic is -2.0872 and the MacKinnon tau statistic is -3.672, you cannot reject the null hypothesis. Hence, the conclusion is that the series is nonstationary. But if the calculated tau statistic is -5.278 and the MacKinnon tau statistic is -3.482, you reject the null hypothesis in favour of the alternative. Hence, the conclusion is that the series is stationary.

*Always use the appropriate critical τ values for the indicated model specification.

How to Perform Unit Root Test in EViews (See here for Stata)

Example dataset is from Gujarati and Porter T21.1

Several tests have been developed in the literature to test for unit root. Prominent among these tests are Augmented Dickey-Fuller, Phillips-Perron, Dickey-Fuller Generalised Least Squares (DFGLS) and so on. But this tutorials limits testing to the use of ADF and PP tests. Once the reader has good basic knowledge of these two techniques, they can progress to conducting other stationarity test on their time series variables.

How to Perform the Augmented Dickey-Fuller (ADF) Test

An important assumption of the DF test is that the error terms are independently and identically distributed. The ADF test adjusts the DF test to take care of possible serial correlation in the error terms by adding the lagged difference terms of the outcome (dependent) variable. For Y_t series, in conducting the DF test, it is assumed that the error term v_t is uncorrelated. But in case where it is correlated, Dickey and Fuller have developed a test, known as the augmented Dickey–Fuller (ADF) test. This test is conducted by “augmenting” the preceding three model specifications stated above by adding the lagged values of the dependent variable.

As mentioned earlier, approaches will be limited to using the ADF and PP tests. Either of these tests can be used and when both are used, the reader can compare the outcomes to see if there are similarities or differences in the results.

1.    Load workfile into EViews.

2.    We are considering only lnpce and lnpdi in natural logarithms.

The Augmented Dickey-Fuller (ADF) Test

Unit root test for lnpce:

·      Double click the lnpce series to open it.

·   Go to View >> Unit root test >> dialog box opens >> Under Test Type, select Augmented Dickey Test

·    Decide whether to test for a unit root in the level, 1st difference, or 2nd difference of the series. Ideally, always start with the level and if we fail to reject the test in levels then continue with testing for the first difference. Hence, we first click on 'Level' in the dialog box to see what happens in the levels of the series and then continue, if appropriate, with the first and second  differences. 

·    Also, the choice of model is very important since the distribution statistic under the null hypothesis differs across these three cases. Therefore, specify whether to include an intercept, trend and intercept, or none in the regression. It is more appropriate to consider the three possible test regressions when dealing with stationarity test. Thus, our demonstration will involve these three options: “none”, “constant”, “constant and trend”.

·      We have to also specify the number of lagged dependent variables to be included in the model in order to correct for the presence of serial correlation. Thus, the number of lags to be included in the model would be determined either automatically or manually. I prefer to allow AIC automatically decide the lag length. Due to the fact that I have a quarterly data, AIC automatically chose 11 lags which I modified to 8.

Consequently, EViews reports the test statistic together with the estimated test regression. The null hypothesis of a unit root is rejected against the one-sided alternative hypothesis if the computed absolute value of the tau statistic exceeds the DF or MacKinnon critical tau values and we conclude that the series is stationary; otherwise (that is, if it is lower), then the series is non-stationary.

Another way of stating this is that in failing to reject the null hypothesis of a unit root, the computed τ value should be more negative than the critical τ value. Since in general δ is expected to be negative, the estimated τ statistic will have a negative sign. Therefore, a large negative τ value is generally an indication of stationarity.

On the other hand, using the probability value, we reject the null hypothesis of unit root if the computed probability value is less than the chosen level of statistical significance.  

·   Having specified the “none” option where both the intercept and trend are excluded in the test regression, the unit root test dialog box is shown thus:

EViews - Unit root test dialog box
Source: CrunchEconometrix

 ·      The ADF unit root test results for the selected regression option, “none” appears as follows:

EViews - Augmented Dickey-Fuller test ("none") option
Source: CrunchEconometrix

 Following similar procedures, the select “intercept” for the ADF unit root test yields:

EViews - Augmented Dickey-Fuller test ("intercept") option
Source: CrunchEconometrix

The result for the “trend and intercept” options for the ADF unit root test is shown below:

EViews - Augmented Dickey-Fuller test ("trend and intercept") option
Source: CrunchEconometrix

·      Do same for the lnpdi series.

The three ADF specifications all confirm that lnpce is nonstationary with a trend which is also a confirmation of the graphical plot. The next thing to do is to run the specifications with the “1^st difference” option, and if the series is still nonstationary, the “2^nd difference” option is conducted.

·      1^st difference with “none” option result:

EViews - Augmented Dickey-Fuller test 1st difference ("none") option
Source: CrunchEconometrix

·      1^st difference with “intercept” option result: 

EViews - Augmented Dickey-Fuller test 1st difference ("intercept") option
Source: CrunchEconometrix

 ·      1^st difference with “trend and intercept” option result:

EViews - Augmented Dickey-Fuller test 1st difference ("trend and intercept") option
Source: CrunchEconometrix

The three ADF specifications all confirm that lnpce is stationary at 1^st difference but at varying significance levels. Given that I am willing to reject the null hypothesis at the 5% level, then the conclusion is that lnpce is stationary at 1^st difference with a constant because it is only at that specification that the null hypothesis of a unit root is rejected. Hence, carrying out a “2^nd difference” test is unnecessary.

·      Again, do same for the lnpdi series.

How to Perform the Phillips-Perron (PP) Test

Phillips and Perron use nonparametric statistical methods to take care of the serial correlation in the error terms without adding lagged difference terms. Procedures for testing for unit root using PP test are similar to that of ADF earlier discussed except for the Test Type options.

Note: The asymptotic distribution of the PP test is the same as the ADF test statistic.

After unit root testing, what next?

The outcome of unit root testing matters for the empirical model to be estimated. The following scenarios explain the implications of unit root testing for further analysis. 

Scenario 1:  When series under scrutiny are stationary in levels? 

If pce and pdi are stationary in levels, that is, they are I(0) series (integrated of order zero).  In this situation, performing a cointegration test is not necessary. This is because any shock to the system in the short run quickly adjusts to the long run. Consequently, only the long run model should be estimated.  That is, the model should be specified as:

 pce_t = 𝛂₀ + bpdi_t + u_t

In essence, the estimation of short run model is not necessary if series are I(0).  

Scenario 2: When series are stationary in first differences?

·    Under this scenario, the series are assumed to be non-stationary.

·     One special feature of these series is that they are of the same order of integration.

·  Under this scenario, the model in question is not entirely useless although the variables are unpredictable. To verify further the relevance of the model, there is need to test for cointegration.  That is, can we assume a long run relationship in the model despite the fact that the series are drifting apart or trending either upward or downward?

·   If there is cointegration, that means the series in question are related and therefore can be combined in a linear fashion. This implies that, even if there are shocks in the short run, which may affect movement in the individual series, they would converge with time (in the long run).

·   However, there is no long run if series are not cointegrated. This implies that, if there are shocks to the system, the model is not likely to converge in the long run.

·   Note that both long run and short run models must be estimated when there is cointegration.

·  The estimation will require the use of vector autoregressive (VAR) model analysis and VECM models.

·  If there is no cointegration, there is no long run and therefore, only the short run model will be estimated. That is, run only VAR no VECM analysis!

·  There are however, two prominent cointegration tests for I(I) series in the literature. They are Engle-Granger cointegration test and Johansen cointegration test.

·  The Engle-Granger test is meant for single equation model while Johansen is considered when dealing with multiple equations. 

Scenario 3: The series are integrated of different order? 

·  Should in case lnpce and lnpdi are integrated of different orders, like the second scenario, cointegration test is also required but the use of either Engle-Granger or Johansen cointegration are no longer valid.

·    The appropriate cointegration test to apply is the Bounds test for cointegration and the estimation technique is the autoregressive distributed lag (ARDL) model.

·    Similar to case 2, if series are not cointegrated based on Bounds test, we are expected to estimate only the short run. That is run only the ARDL model.

·   However, both the long run and short run models are valid if there is cointegration. That is run both ARDL and ECM models.

In addition, there are formal tests that can be carried out to see if despite the behaviour of the series, there can still be a linear combination or long run relationship or equilibrium among the series. The existence of the linear combination is what is known as cointegration. Thus, the regression with I(1) series can either be spurious or cointegrated. The basic single equation cointegration tests are Johansen, Engle-Granger and Bounds cointegration tests. These will be discussed in detail in subsequent tutorials.

[Watch video clip on performing ADF stationarity test in EViews]

In conclusion, I have discussed what is meant by nonstationary series, how can a series with a unit root be detected, and how can such series be made useful for empirical research? You are encouraged to use your data or the sample datasets uploaded to this bog to practise in order to get more hands-on knowledge.

Please post your comments below….